Some basic expressions

• Plaintext: Some information that is readable, unencrypted.
• Ciphertext: Some information that is not readable, encrypted.
• Algorhitm: Some function(s) that make plaintext to ciphertext.
• Key: Some information that combined with an algorithm transforms plaintext to ciphertext.
• Symmetric encrpytion: The same key is used to encrypt and decrypt.
• Assymetric encryption: Different key is used to encrypt and decrypt.
• Publickey encryption: The same as assymetric encryption.

Classical ciphers - Caesar cipher

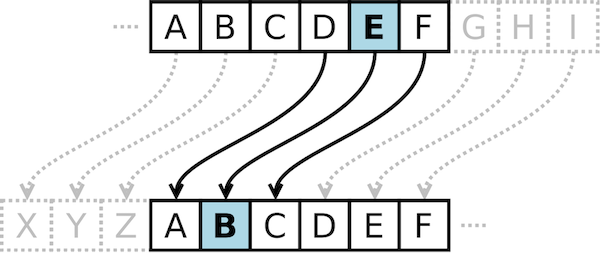
The Caesar cipher is a substituion cipher, which means that each letter in the plaintext get substituted with another letter to create the ciphertext. The Caesar cipher is based on the shift principle, so it shifts every letter in the plaintext 3 places to the right to create the ciphertext.

ABCDEFGHIJKLMNOPQRSTUVWXYZ / Normal alphabet

DEFGHIJKLMNOPQRSTUVWXYZABC / Ceasar alphabet

HELLO
KHOOR

To break the Caesar cipher you can just shift all the letters in the ciphertext 3 places to the left.

If you want to make it more secure you could adjust the shift value from 3 to a secret value that only you and the recipent of the message know, i.e creating a secret-key.

Read more about Caesar cipher here: https://www.dcode.fr/caesar-cipher

Classical ciphers - Vigenère cipher

The Vigenère cipher surfaced around the 1600, 1500 years after the Ceasar cipher. Its similar to the Caesar cipher, but instead of a fixed value of the shift, the shift value is determined by a key.

If you have the key "BCD", it means shift values of "2,3,4".

HELLO
IGOMQ

So as we can see, the Vigenère is far more advanced than the Caesar cipher due the fact that the shift value is constantly changing. But there are a couple of problems here: - If the key is shorter than the plaintext we might start to se repeating patterns, and can start guess the length of the key. Picture the key 'BCB', which gives shift values of '2,3,2', and plaintext 'SOS HELP ME SOS'.

SOSHELPMESOS
TQTIGMQOFTQT

The pattern 'TQT' repeats at interval of 9, which we can use to assume the keylength is 9, or a value divisible by 9, i.e 3.

• The way we substitute does not change the order or the numbers a letter is represented in the ciphertext versus in the plaintext, it just changes the letter itself. This fact makes us vulnerable to frequency analysis. We know that i.e the letter 'e' is the most common letter found in the english language. So if we find alot of the same letters in the ciphertext we might assume that the plaintext equivalent is 'E'. If we proceed doing this for the most common letters in the language we will end up with a educated guess of what the key is.

Read more about Vigenère cipher here: https://www.dcode.fr/vigenere-cipher

How ciphers work - The permutation

Permutation is a function that transforms a letter, or set of bits, in such a way that each letter has a unique reverse. In the example of the Ceasar cipher the permutation is the shift of 3. It is also essentials that each permutation itself is unique: We can not have a cipher where both letter 'A' and 'B' is substituted with to 'D' because then we will not be able to decrypt the ciphertext.

To be secure a permutation should satisfy some criteria:

• Permutation should be determined by the key. If the key is kept secret, the message is kept secret. Like in the Vigenère cipher, without the key, you will noe know the shift values and can not easily decrypt the message.
• Different key should result in different permutation. If multiple keys results in same permutation it will be easier to guess or break one of the keys that can decrypt the message.
• The permutation should look random. An attacker should not be able to draw any patterns from the ciphertext. If we are using the Vigenère cipher and find that 'A' encrypts to 'C', we also know that 'B' encrypts to 'D', 'C' to 'E' and so on. This is a pattern that is easy to predict because we know that there is a shift of 2. With a random permutation the only thing we can deduce from 'A' encrypts to 'C' is that no other letter is encrypted to 'C'.

How ciphers work - The mode of operation

Mode of operation is an algorithm that uses a permutation to process a message of random length. In the example of the Cesar cipher, the mode of operation is to repeat the same shift of 3 permutation for each letter in the message. A cipher's mode of operation can mitigate the problem that we get when multiple occurenses of a letter in the plaintext get revealed in the ciphertext (thus make us vulnerable to frequency analysis), like the Caesar cipher (3-shift) example where 'HELLO' is encrypted to 'KHOOR'. The mode of operation of the Vigenère partially defeats this, and if the keylength is equal to the length of the plaintext we can make frequency analysis difficult.

Python code to show Caesar cipher at work

To get a feeling of how it works I have created a python snippet that can be used to encrypt/decrypt Caesar cipher texts.

#!/usr/bin/env python3

alphabet_0 = 'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'
alphabet_3 = 'D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','A','B','C'
encoding_dict = dict(zip(alphabet_0,alphabet_3))
decoding_dict = dict(zip(alphabet_3,alphabet_0))

def encrypt (plaintext):
    ciphertext = ""
    for letter in plaintext.upper():
        if letter.isalpha():
            ciphertext += (encoding_dict.get(letter))
    return ciphertext

def decrypt (ciphertext):
    plaintext = ""
    for letter in ciphertext.upper():
        if letter.isalpha():
            plaintext += (decoding_dict.get(letter))
    return plaintext

print(encrypt("HELLO"))
print(decrypt("KHOOR"))

When the code above is run it will output the following:

KHOOR
HELLO

Process finished with exit code 0